3.パスカルの三角形と二項定理の証明 高等学校において,二項定理を早々に扱うに は,議論の余地も残ると思うが,順列や組合せ は実社会で遭遇する場面も多く,記号 や を早期に導入することは無理なことではな いと思われる。一般にも,(a b) をn 回掛けたとき,a を r 回選ぶと,残りの n-r 回は自動的に b が選ばれるので,(a b) n の展開式における,a r b n-r の項の係数は, n C r となります。このことから, n C r は二項係数と呼ばれることがあります。 パスカルの三角形 二項係数を並べると,次のようになります1章 パスカルの三角形、二項定理、Catalan数 まずは、いきなり Excelの計算式定義から。 行・列は R1C1 形式で。 1行目、1列目には1を入れる。 2行2列目に計算式 =R 1CRC 1 を入れる(これは、直上と直左を足したもの)。 これを、1行1列目を頂点とした
二項定理 パスカルの三角形 大人が学び直す数学
パスカルの三角形 二項定理 問題
パスカルの三角形 二項定理 問題- 吉田武「 オイラーの贈物 」の「 基礎理論 (Basic Theory)」における 二項定理 (binomial theorem)または 二項展開 (binomial expansion) の解説は パスカルの三角形 (Pascal's triangle)の説明を導入部とします。二項定理からほんの少し発展させた授業展開 している教科書は、平均的な教科書に比べて取りあげられていない内容が結構ありま す「パスカルの三角形」もその1例ですが「パスカルの三角形」の持つ性質を見つけようとい。 11 11 1 1一般的な形へ 2項
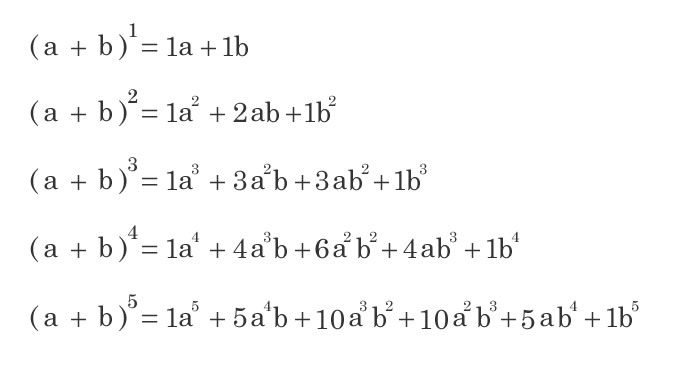



二項定理 パスカルの三角形 優技録
二項定理によると、` (ab)^n `を展開したときの ` a^(nr)b^r `の係数は ` {}_n C_r `でした。 これをパスカルの三角形に当てはめてみましょう。 さっきのパスカル三角形と比べてみてください。 n段目と(n1)段目に注目すると、次の図のようになります。パスカルの三角形の各行は二項係数そのもの。 つまりパスカルの三角形を書けるようになれば、二項定理の問題が出てきても係数を簡単に計算できるわけです。 例えば $ (xy)^6$ はパスカルの三角形の六段目から (xy)^6 = x^6 6 x^5 y 15 x^4 y^2 x^3 y^3 15パスカルの三角形と多項定理 中川湧介 東狐太朗 ・動機 11n と二項定理の係数には関係があるということを知り、どのような関係があるのか、 またどうしてそのようになるのか疑問に思ったから。 ・パスカルの三角形とは? パスカルの三角形とは、二項係数を三角形状に並べたもの。
数学の二項定理の問題なのですが・・ (2x+3y)^8 x^6y^2) という問題の解き方が理解できません。 学校の先生に聞いてみたんですけど その後自分で解いたら理解できてなくて・・ 先パスカル全集 第一巻 『数三角形論』 関連分野 数学的帰納法、二項定理、数列 学習指導要領との関連 高等学校 数学Ⅲ 「極限」 高等学校 数学A 「集合と論理」「場合の数と確率」 高等学校 数学B 「数列」 対象学年 高等学校2年、高等学校3年 ここでは、二項定理を知った上で、パスカルの三角形をもう一度見直してみます。 二項定理とパスカルの三角形 パスカルの三角形とは、次のように、 n 乗の係数を並べたものでしたね。 begin{array}{cccccccc
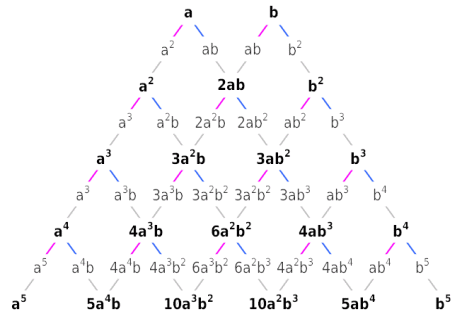
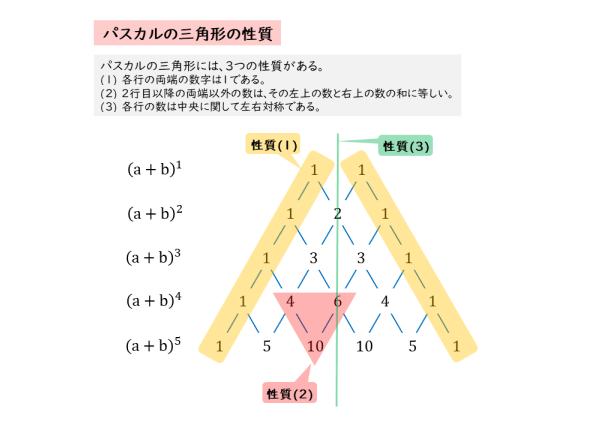
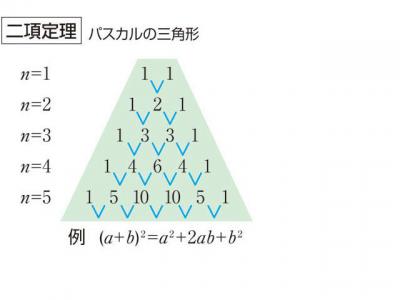
表紙に戻る パスカルの三角形拡張 今、2つの項をもつ式を次数を上げながら展開していきます。 (ab) 1 = a b (ab) 2 = a 2 2ab b 2 (ab) 3 = a 3 3a 2 b 3ab 2 b 3 (ab) 4 = a 4 4a 3 b 6a 2 b 2 4ab 3 b 4 (ab) 5 = a 5 5a 4 b 10a 3 b 2 10a 2 b 3 5ab 4 b 5 これらの展開係数を三角形に並べると以下のようになりこのように, n C r は二項定理の係数として現れるため,二項係数とも呼ばれます. さて,実はこの n C r を パスカルの三角形と呼ばれる配置で並べると,二項係数の間の関係式が見えてきます.よく考えると、二項定理を使って、y=χ n の導関数が求まるんだから当然かな。 S:そうか。 パスカルの四角形を見ると、f n '(χ)=nf n1 (χ) が成立するから、微分をしているということですね。




考える家庭教師



1
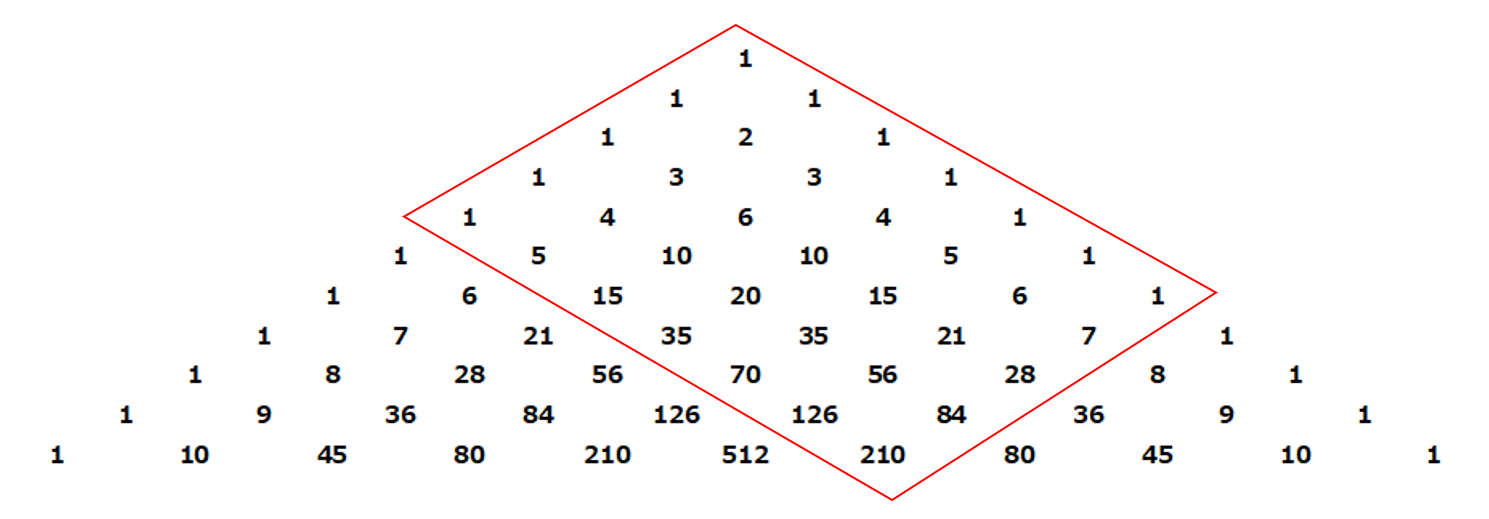
次は、 パスカル の三角形に関連する 級数 公式。 パスカル の三角形については『 wikipediaパスカルの三角形 』参照。 パスカル の三角形から二項係数が計算できることを数式で表してみましょう。 まず、三角形で水平に(固定された n で)見て両端が1な 以上、組み合わせ・二項係数の覚え方として、パスカルの三角形や、組み合わせの考え方を紹介してきました。 組み合わせは確率を考えるときに役立ちますが、二項定理は多項式の テイラー展開 にも役立つもので、\(_n C_k\)を理解することは長期的に価値組合せ、つまり、二項係数の nCr の r と n − r は、多項定理から分かるように、交換可能な対称性を持っているので、 n = x y と置き直すと、 x yCx = x yCy と書け、さらに、パスカルの三角形が 1 の和で構成されていることをよく観察すると、 x yCx = x ∑ k1




パスカルの三角形 数学における二項係数の三角形配列の計算 各番号は 直接上記 2 つの合計です 正規分布 ベクトル のイラスト素材 ベクタ Image



2
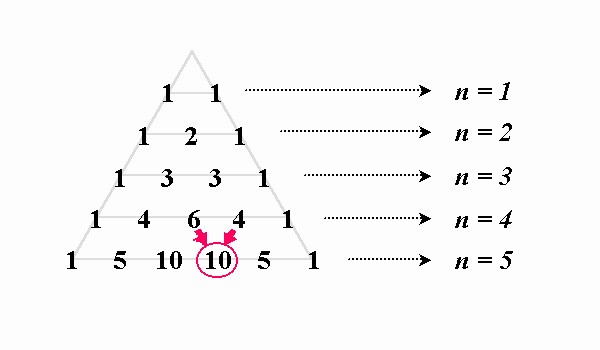
パスカルの三角形とは、最上段に1 を配置し、 それより下の段に右上の数と左上の数の和を置いた三角形のことである。 これは二項定理と深い関わりがあり、パスカルの三角形の n 段目に対して、(ab) n1 の係数が対応している。二項係数の有名公式一覧と2つの証明方針 レベル ★ 最難関大受験対策 場合の数 二項定理 更新日時 二項係数の有名公式を紹介していきます。 二項係数の関係式を証明するための2通りのアプローチを紹介します。 目次パスカルの三角形 二項係数の値は、 組み合せについての定理 n C r = n-1 C r + n-1 C r-1 を図式化した「パスカルの三角形」を書くと、 容易に把握できる。 数値化すると、



2



パスカルの三角形の性質とフラクタル 高校数学の美しい物語
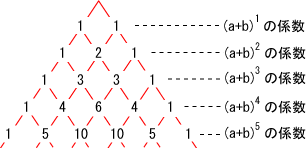
パスカルの三角形 記号nCr の意味 二項定理 − 8 − 第1章 方程式・式と証明「整式・分数式の計算」 数学Ⅱ 講師 二項定理 矢作 裕滋 第4回 学習のこの三角形を書いた人は、もっと昔からいたみたいだけど、確率と合わせたのは、たぶんパスカルさんが初めて。 三角の中に並んでる数字には「二項係数」って名前が付いてます。 a と b、2つにくっついてる数字だから「二項係数」。二項定理において,a=1,b=1とすると,パスカルの三角形において,各段の数の総和がすぐに分かる。 例えば,(1+1) 4 =1 4 +4 3 ×1 1 +6 2 ×1 2 +4×1 3 +1 4 だから 1+4+6+4+1=2 4 =16 また,二項定理において、a=10,b=1とすれば,次のような性質も




差がつくポイント 二項定理はイメージで覚えろ 重要なポイントと活用場面を総まとめ 青春マスマティック



2
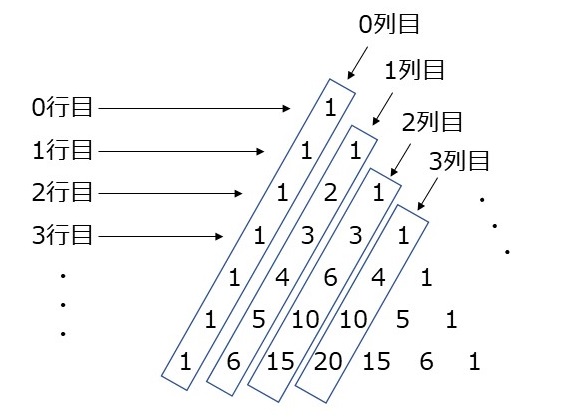
二項係数の和 r 行目k 列目にr 行目k1 列目を加えると、 r1 行目k1 列目になる: 組み合わせの数としての解釈:r1人からk1人選ぶ 二項定理とは? 証明や応用問題の解き方をわかりやすく解説! 21年2月19日 この記事では、「二項定理」についてわかりやすく解説します。 定理の証明や問題の解き方、分数を含むときの係数や定数項の求め方なども説明しますので、この記事を通して この数の三角形がパスカルの三角形と呼ばれているのは、パスカル Pascal, Blaise, が1654年から1658年頃までの間に書いたとされる一連の論文において算術三角形を計算原理とした数列の計算法や二項展開法を整理するとともに組み合わせ論、確率論の基礎を確立し、その後の理論の発展の



ホッケースティック恒等式 思考力を鍛える数学



パスカルの三角形は二項定理に対応しますが パスカルの三 Yahoo 知恵袋
二項定理 を展開していくと の 個から を 個選べばいいので となります。よって、 の係数は となります。 パスカルの三角形 二項定理は覚えにくという方はパスカルの三角形という方法で覚えましょうパスカルの三角形のもっとも簡単な応用は 二項展開 です.これはつぎの 二項定理 に基づいています. 二項定理: (x y)n = n ∑ k=0nCkxkyn−k (x y) n = ∑ k = 0 n n C k x k y n − kパスカルの三角形 として、とっても有名です。 ただし、三角形というくらいですから、(このままではパスカルの正方形! ? ) ちょっと回転(かいてん)させるのです。 では、パスカルの三角形をきちんとかいてみましょう。 さて、 2項定理 でこれ




二項展開とパスカルの三角形 オイラーの公式目指して Youtube




パスカルの三角形と二項定理による展開との関係とは 二項係数の性質を証明 遊ぶ数学
二項定理? に関するもの プログラマ専用SNS ミクプラ 二項定理? に関するもの フォーラム (掲示板)ルールはこちら ※コードを貼り付ける場合は code と /code で囲って下さい。 詳しくは こちら 二項定理? に関するもの はじめまして数学ii 改訂版プリント# 4 年 組 号 氏名 パスカルの三角形、二項定理 組合せc の計算 8c3 = 8 × 7 × 6 3 × 2 × 1 8 × 7 ×/6 /3 1 1/3 ×/2 1 × 1 = 8 × 7 = 56 その他の例 9c2 = 9 × 8 2 × 1 9 ×/8 4 1/2 × 1 = 9 × 4 = 36 6c4 = 6 × 5 × 4 × 3 4 × 3 × 2 × 1 3/6 × 5 ×/4 1 ×/3 1 1/4 ×/3 1 ×/2 1 × 1 = 3 × 5 = 15 5c0 = 1, 9c0



数学 基礎 パスカルの三角形と展開公式の係数




高校数学 二項係数ncrの等式とパスカルの三角形 受験の月




パスカルの三角形でプラスの答え方はわかるんですけどマイナスのやり方がわからない Clear



1




二項定理とは 東大生が公式や証明問題をイチから解説 高校生向け受験応援メディア 受験のミカタ




二項定理のパスカルの三角形を利用する問題があるのですが Clear




パスカルの三角形の性質 数学ii By ふぇるまー マナペディア




パスカルの三角形と二項定理 Our School




パスカルの三角形 数学a フリー教材開発コミュニティ Ftext




二項定理を超わかりやすく解説 公式 証明 係数 問題 理系ラボ




二項定理ってなんだよ 多項定理ってなんだよ ってなっている君へ



二項定理




パスカルの三角形 Wikipedia




二項係数の和を求める2通りの方法とは 大学入試数学の考え方と解法




数 二項定理 パスカルの三角形 理由付き オンライン無料塾 ターンナップ Youtube




二項定理の公式を超わかりやすく証明 係数を求める問題に挑戦だ 応用問題も解説 遊ぶ数学



2



2



パスカルの三角形 Wikipedia




先生 二項定理がよくわかりません 怜悧玲瓏 高校数学を天空から俯瞰する
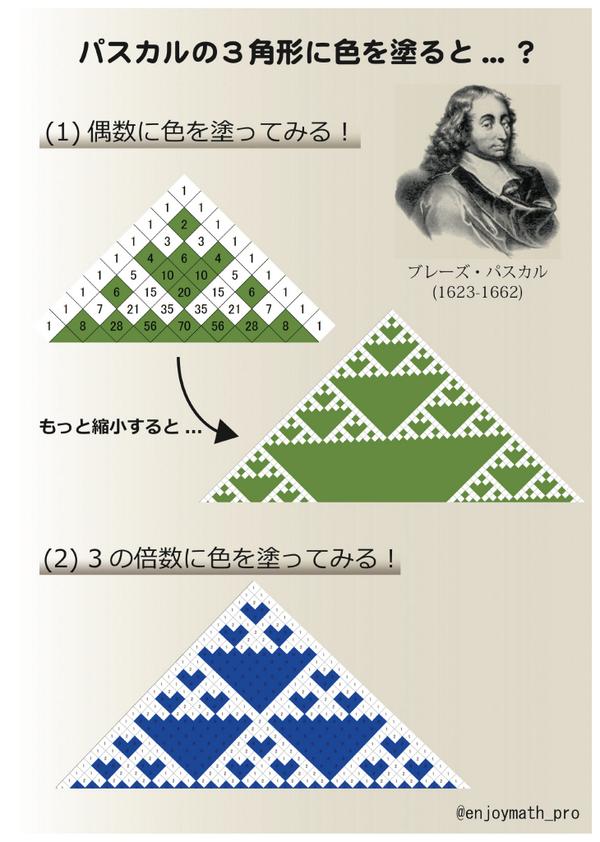



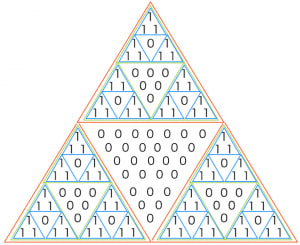
高校数学を100倍楽しく 数a 場合の数 二項定理と一緒によく登場するパスカルの三角形ですが 実はとても面白い性質を持っています ゚d゚ 実際に色を塗ってみると感動するかもしれませんよ このような図形のことを フラクタル と言ったりします
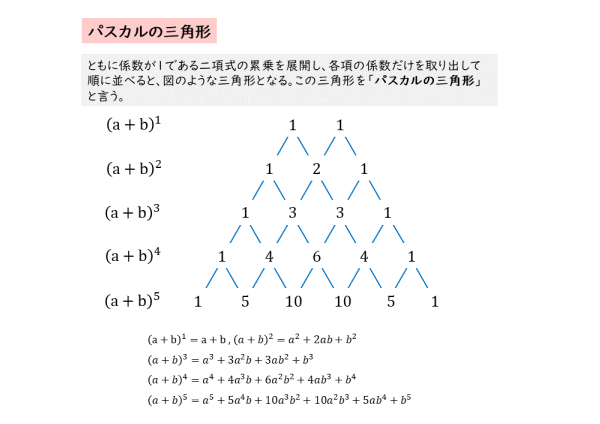



式と証明 パスカルの三角形について 日々是鍛錬 ひびこれたんれん



このもんだいの 2 3 のやり方をわかりやすく教えてください Yahoo 知恵袋




東大数学ー二項係数の難問 09年ー 虚空が数学をやるブログ




パスカルの三角形
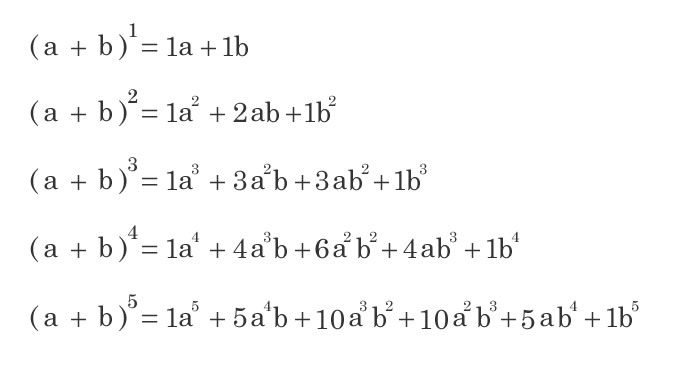



二項定理 パスカルの三角形 優技録



辞書 パスカルの三角形 わかりmath
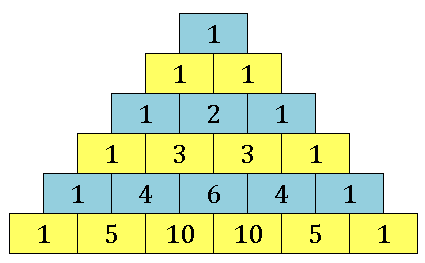



パスカルの三角形と 2 項定理 多項定理




二項定理 数スタ




A B が A 4a B 6a B 4ab B Clear




パスカルの三角形 Wikipedia




数ii 二項定理 高校生 数学のノート Clear



パスカルの三角形 二項定理 保谷高校数学科



式と証明 パスカルの三角形について 日々是鍛錬 ひびこれたんれん




二項定理を超わかりやすく解説 公式 証明 係数 問題 理系ラボ



二項定理 Taustation



二項定理とは 証明や応用問題の解き方をわかりやすく解説 受験辞典



思索の散歩道 パスカルの三角形拡張




二項定理の説明で 写真の蛍光ペンの部分がどうしても理解出来ないというか なぜこうなる Clear
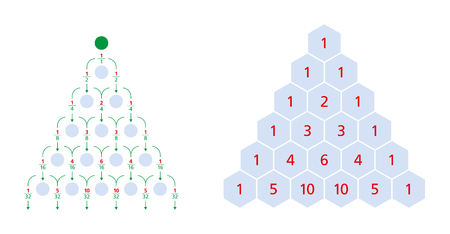



パスカルの三角形 数学における二項係数の三角配列 各番号は 直接上記 2 つの合計です 正規分布 ベクトル のイラスト素材 ベクタ Image



難しい二項定理の中に隠れた 大量の三角形を見てみよう




この問題がわかりません パスカルの三角形を使う問題です Clear




Square 1 Ab N See How To Solve It At Qanda



2




二項定理 パスカルの三角形 齊藤数学教室 算数オリンピックから大学数学入門



パスカルの三角形



パスカルの三角形とシェルピンスキーギャスケット




二項定理 Dinop Com



パスカルの三角形 Tomの日常




パスカルの三角形 説明



二項定理とかパスカルの三角形がよくわかんないです どんな風に解くとか Yahoo 知恵袋



Kanazawa U Repo Nii Ac Jp Action Repository Uri Item Id File Id 26 File No 1



Java パスカルの三角形を使って組合せを求める ヽ ゝ Fantom の 開発blog




パスカルの三角形 Wikipedia
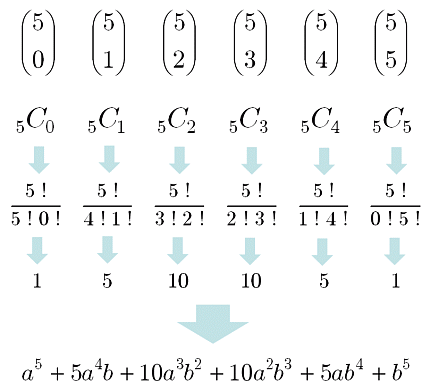



二項定理 二項係数の性質を研究する 素数との関係 大人が学び直す数学




二項定理とは 公式と係数の求め方 応用までをわかりやすく解説



パスカルの三角形が二項係数になるのはなぜですか Quora



1



2




微分 パスカルの三角形と微分 二項定理とともに X Nの微分公式を証明 N乗まで一般化しよう Youtube
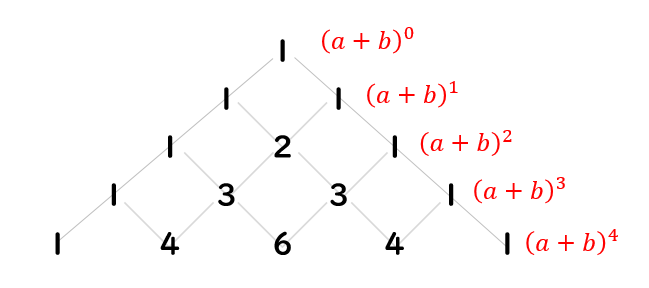



パスカルの三角形の作り方 覚え方 二項定理の係数をマスターせよ 数スタ



2
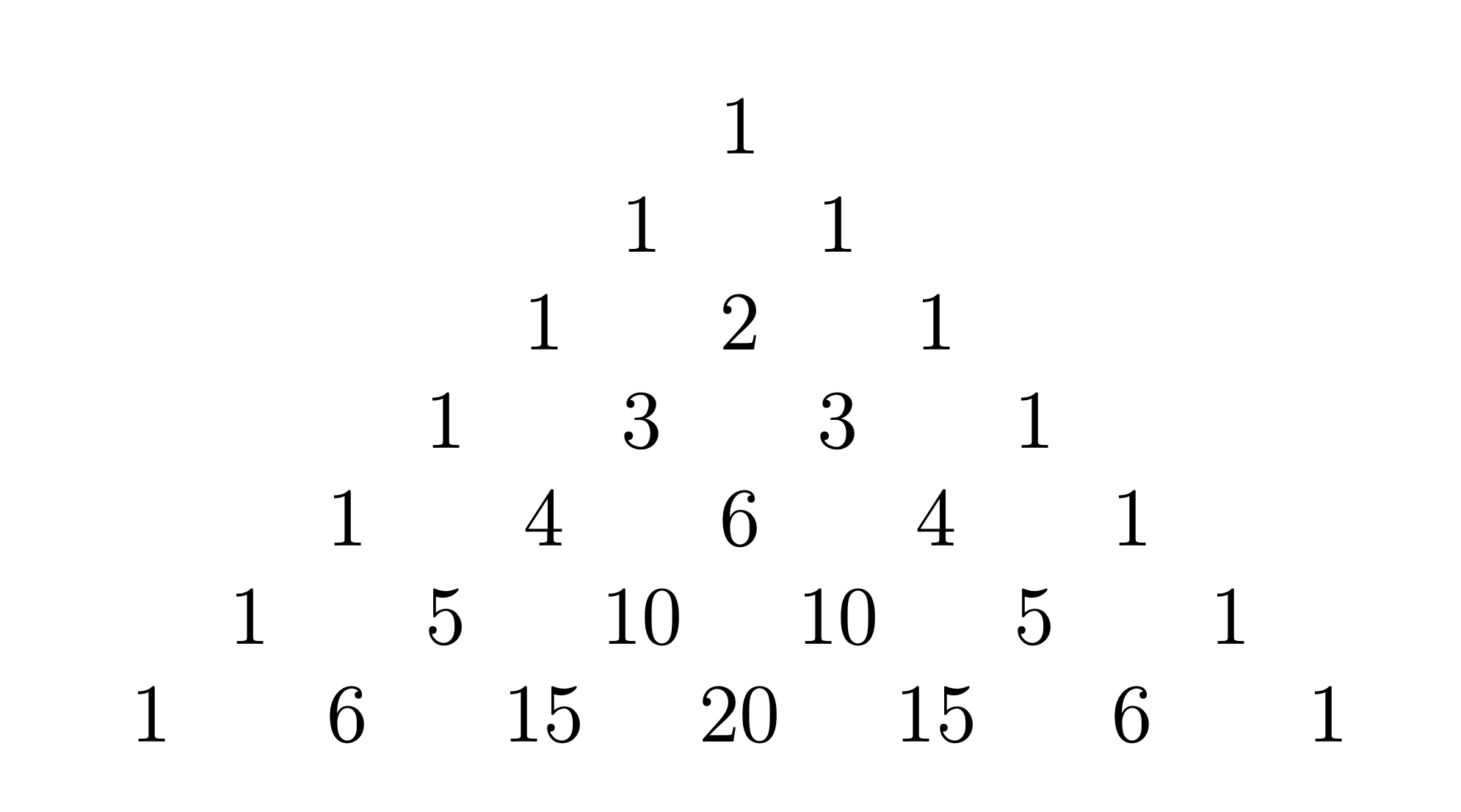



パスカルの三角形と二項係数 Gleamath Com
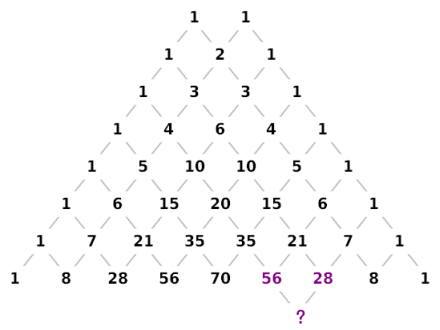



二項定理 パスカルの三角形 大人が学び直す数学




二項定理 パスカルの三角形 大人が学び直す数学
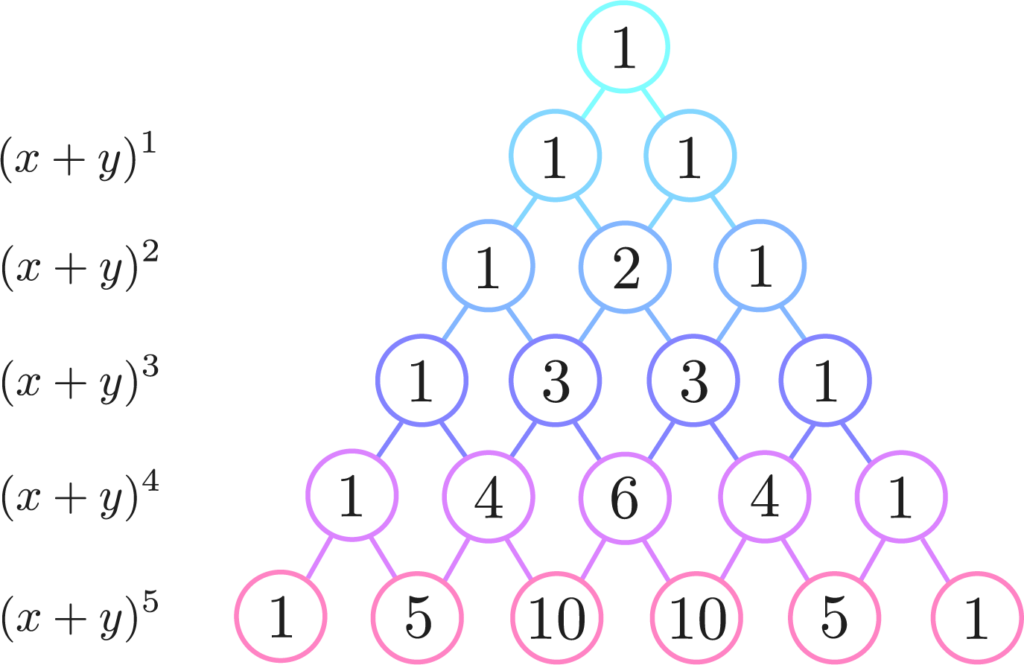



二項定理 そして多項定理について ゆっくり機械学習




二項定理の公式と証明をわかりやすく解説 公式 証明 係数 問題



二項分布
.jpg)



二項定理のしくみと意味 A B のn乗 高校数学なんちな



パスカルの三角形とシェルピンスキーギャスケット




パスカルの三角形 Wikiwand




二項定理 Wikipedia




パスカルの三角形 数学における2項係数の三角形配列 各数値は 上の2つの値の合計です 標準分布 ベクター画像 のベクター画像素材 ロイヤリティフリー



にこう ていり 二項定理 ニカウ 広辞苑無料検索 大辞泉



パスカルの三角形とシェルピンスキーギャスケット



2



パスカルの三角形と最短経路 思考力を鍛える数学




パスカルの三角形にたくさん出てくる数 3003 Tsujimotterのノートブック



1



二項定理 にこうていり の意味 Goo国語辞書



パスカルの三角形 二項定理 保谷高校数学科




二項係数 Tutorialcup



二項係数とパスカルの三角形の関係 Qiita



2



パスカルの三角形の不思議な性質7個 パスカルの三角形に秘められた不思議な性質 やまでぃーのブログ



パスカルの三角形




二項係数




場合の数 組み合わせ 二項定理 中学数学と高校数学のつなぎ目 Web朝倉学校 数学 理科 第7回後半 発展編 15分 年3月10日 朝倉幹晴 船橋市議 予備校講師 Youtube
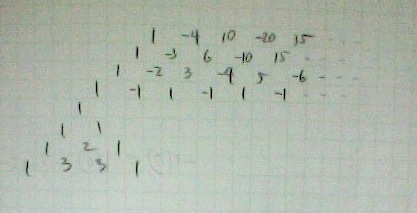



二項定理を負の数に拡張する 6 ワイドスクリーン マセマティカ



パスカルの定理と二項定理の違いはなんでしょうか 基本7のパスカルの定理を Yahoo 知恵袋




組み合わせの公式2 高校数学 二項定理周辺の公式 身勝手な主張




二項定理を超わかりやすく解説 公式 証明 係数 問題 理系ラボ



0 件のコメント:
コメントを投稿